From the illustration in Trivia 6, you must have gotten the idea that all what we see, is above the horizon. Wherever you live, you have your own horizon. Imagine a person 1.7 m tall, lying somewhere on the Earth that has a circumference length of 40,074 kilometers. That person has covered a surface of 0.0004% of the length of the circumference around the Earth. It would be necessary to have 24 million people lying on the equator to trace the circumference of the Earth.
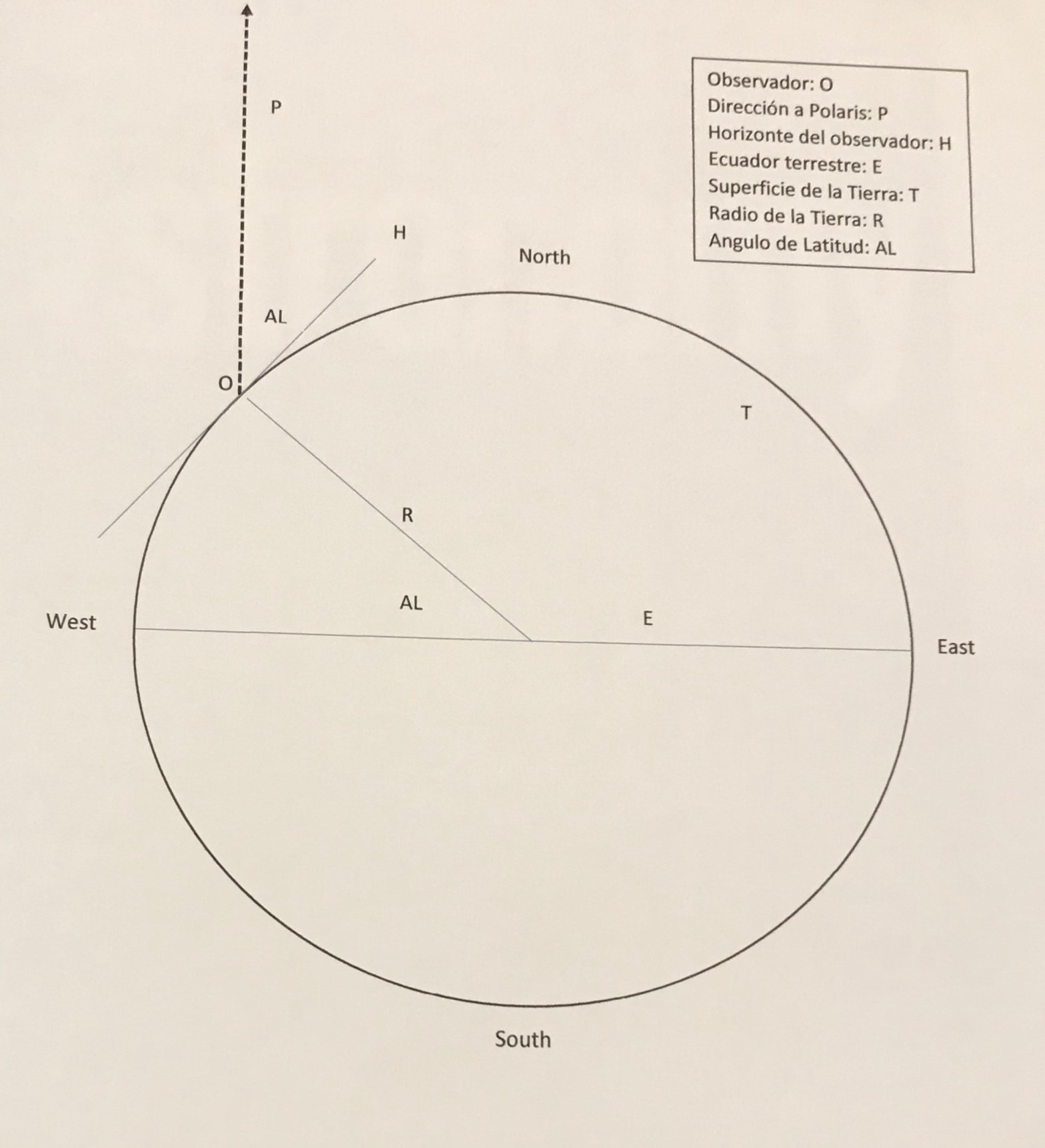
In the picture above, H is the horizon where you are standing as an observer O, at a latitude angle AL. Notice the latitude in this illustration is North, indicated by the Radius R of the Earth and the Equator E. The direction P indicate that you looking at the polar Star, Polaris. The angle of your latitude is also the angle formed by the horizon line and the direction to Polaris. The celestial equator is perpendicular to the dotted line in direction to Polaris. Recall from the illustration in Trivia 6, the Zenith is directly above you, perpendicular to the horizon. This indicates that the prolongation of the Radius of the Earth at your observing site, is the Zenith. The angle between the Zenith and the dotted line to Polaris is 90o – AL. Practically speaking, that would be the angle you will find by stretching one arm towards Polaris, and the other arm towards the Zenith. If you have a telescope, point it to Polaris; the angle the telescope makes with the “ground” (your horizon) is the same as your home latitude. The opposite direction of your telescope will be perpendicular to the equatorial circle, which is the maximum circle around the Earth that divides North and South.
In the next Trivia, I will show you how to locate celestial objects using the celestial coordinates. Stay tune.